Tunneling is a process by which particles (actually, waves) can penetrate and proceed through barriers that have too high energy for classical transmission. Tunneling is strongest for light particles and thin and low barriers. Tunneling is most relevant for hydrogen and deuterium in chemical reactions due to their low mass. While the reaction rate decreases with decreasing temperature for classical chemical reactions, the tunneling rate is independent of the temperature. The over-the-barrier mechanism is always faster for high temperatures than the tunneling process. At low temperatures, tunneling is faster. In the intermediate range, temperature-assisted tunneling occurs, which is particularly interesting and challenging to calculate. A recent review on the calculation of tunneling rates is given in [1], a more light-weighted discussion (in German) in [2].
We use instanton theory to calculate tunneling rates. On the one hand, it is accurate enough to calculate rates in the deep tunneling regime [3]; on the other hand, it is efficient enough to treat systems with a few tens of atoms. We even applied it to systems with many thousand atoms (combined with the QM/MM approach), 78 of which were allowed to tunnel [4].
An instanton represents the most likely tunneling path at a given temperature. It is a saddle point in the space spanned by closed Feynman paths. We adapted our geometry optimizer DL-FIND to search for instantons. Using that, we achieved near-quadratic convergence behavior [5]. A variable integration grid significantly reduced the number of grid points (control points) required [6].
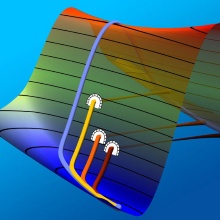
Focusing on astrochemistry [7], we used instanton theory to investigate the formation of H2 in space. The figure above shows the delocalization of atoms during the addition of a hydrogen atom to a benzene molecule. We showed how tunneling can explain the deuterium enrichment in interstellar methanol [3] and demonstrated that atoms heavier than hydrogen (carbon, in fact) can participate in the tunneling [8]. We also used instanton theory to provide a well-defined measure of the tunneling path length in the decay of carbenes [9] and to demonstrate how tunneling synchronizes the proton movement in Grotthuss chains [10]. Meanwhile, most of our effort goes into improving the method in terms of computational efficiency.
Our work concerning the simulation of quantum mechanical tunneling of atoms was funded generously by the ERC project TUNNELCHEM.