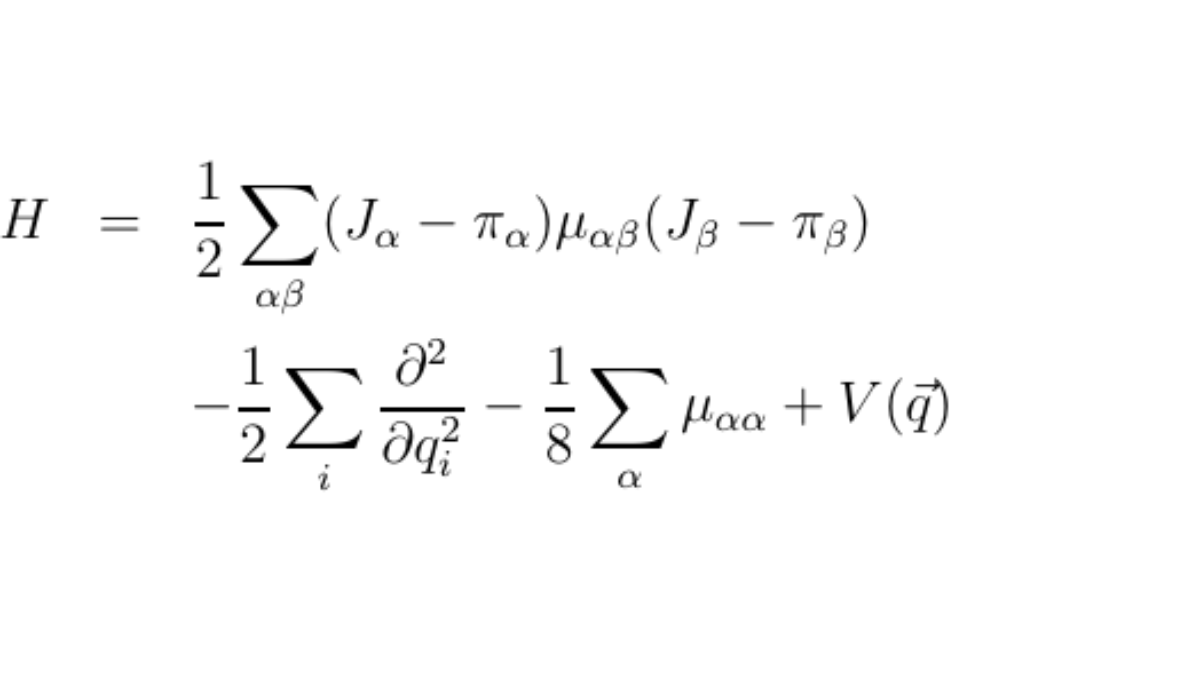All programs needed to solve the vibrational Schrödinger equation are written by ourselves and very much effort goes into the development of new theories and methods. An accurate variational calculation of any (ro)vibrational spectrum requires two aspects, which are in the midst of our research and which are relevant for all other parts of our program.
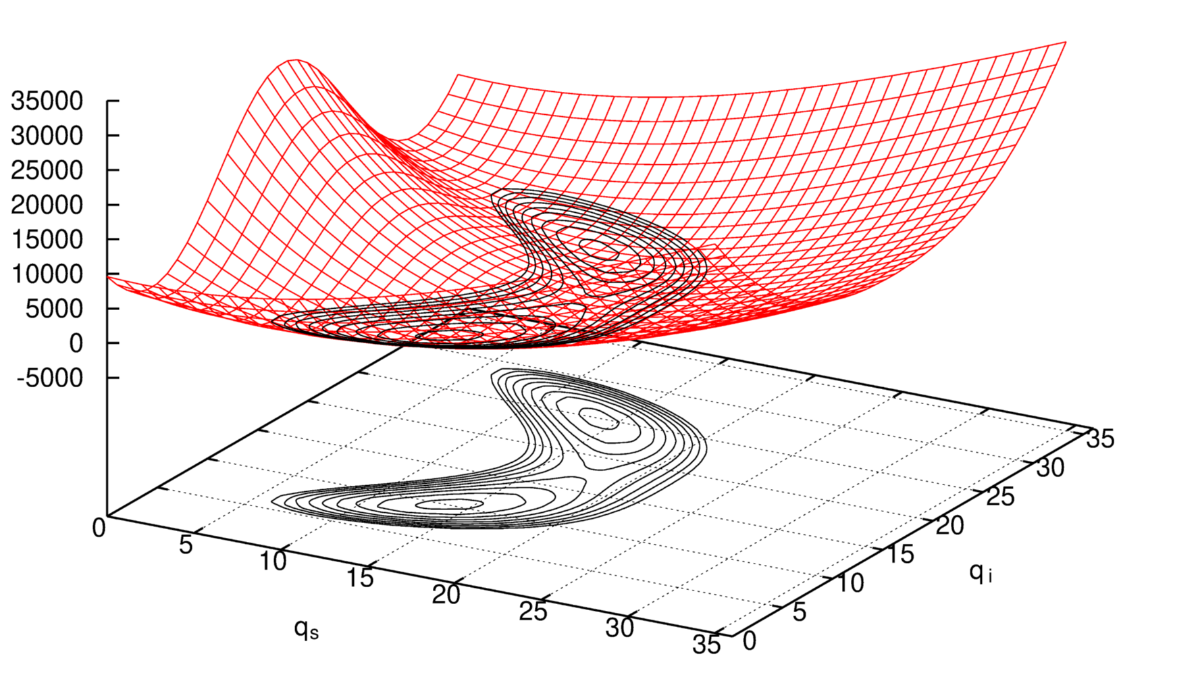
The first one concerns the efficient though accurate evaluation of a multidimensional potential energy surface (PES). It is the so-called curse of dimensionality, which prohibits a complete determination of them, i.e. the number of electronic structure single point calculations grows extremely fast and thus requires some kind of expansion. We employ the n-mode expansion, which we usually truncate after the 4th order terms. Our XSURF program (1) can handle any kind of symmetry and offers many options to compute energy, dipole and polarizability surfaces for systems as large as about 20 atoms (2) . These surfaces are represented in terms of grid points and can be transformed by a highly efficient fitting procedure to an analytical sum-of-products form by our POLY program (3) or into different coordinate systems.
Once an accurate PES has been determined, we solve the nuclear Schrödinger equation based on the Watson operator, which constitutes the 2nd aspect. In a first step we optimize the basis functions to be used and employ vibrational self-consistent field (VSCF) theory, which is the analog to Hartree-Fock theory in electronic structure theory, for doing so. Based on the solutions of VSCF theory we then use vibrational configuration interaction (VCI) theory (4, 5), which has been optimized in our group with respect to CPU-time and memory requirements. Our VCI program exploits symmetry even for non-Abelian molecules and can include high-order vibrational angular momentum terms.
As soon as a correlated wavefunction has been determined, it can be used for many other aspects including the calculation of (ro)vibrational intensities (6), Franck-Condon factors (7), vibrationally averaged properties and so on. Currently, we are actively working on the development of new methods concerning all aspects listed above. These comprise the inclusion of any coordinate systems, the acceleration of the vibration correlation calculations (8, 9), the improved calculation of rovibrational line intensities (10) and related topics.